Matematika za svakoga

U nekom gradu postoji n policijskih postaja( n>=4). U svakoj znaju po neki podatak važan za hvatanje nekog kriminalca. Dokazati da poslije 2n - 4 telefonskih razgovora sve postaje mogu znati sve podatke. (U jednom razgovoru sudjeluju samo dvije postaje.)(Zadatak je preuzet iz knjižice 'Najteži zadaci' iz serije 'Matematika u džepu', a u izdanju 'Tehničke knjige', Beograd)

Postavljanje zadatka:
- Jasno je da kad dvije stanice "razgovaraju", jedna na drugu prenesu svoje informacije.
- Također je jasno da postaja A može doći do informacija postaje B bez međusobnog kontaktiranja, a preko treće stanice C koja je već kontaktirala s jednom od njih.

Na osnovi ovih postavki postavljam prvi model rješavanja:
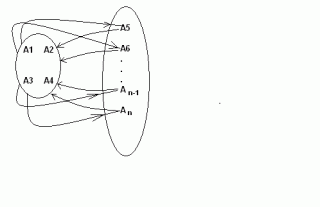
Imamo stanice A1, A2,..., An. Uzmimo da prva stanica A1 razgovara sa preostalih n-1 stanica. Nakon razgovora sa posljednjom stanicom An, prva i posljednja stanica raspolažu sa svim potrebnim informacijama. Sada je dovoljno još da prva stanica opet razgovara sa svim stanicama osim posljednje (An) koja već sve zna, da bi sve stanice doznale sve informacije.
Po ovom modelu potrebno je (n-1) + (n-2) = 2n - 3 razgovora, no to nije rješenje zadatka! Mi tražimo broj 2n-4!

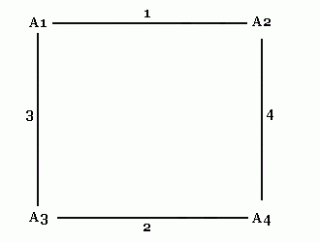
Nemam nikakve ideje, zato krećem od najjednostavnijeg primjera kada imamo četiri stanice(n=4). Lako je vidjeti da je dovoljno obaviti 4 razgovora za potpunu razmjenu informacija, a to odgovara formuli: 2 x 4 - 4 = 4. Pogledajmo sliku:

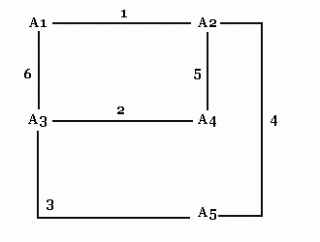
Zatim nastavljam sa n=5. Shema je ova:

Brojevi na linijama označavaju redoslijed razgovora. Vidljivo je da četiri stanice nisu odmah obavile onih četiri razgovora - nakon prva dva razgovora, A2 i A3 su kontaktirali sa A5 i tek nakon toga razgovarali su A1 sa A3 i A2 sa A4. Razmišljajući dalje, uočavam da sam mogao i promijeniti redoslijed razgovora sa istim učinkom, dobivam slijedeću shemu:

I ovdje prije "kompletiranja" prve četiri stanice radim razgovore sa A5.

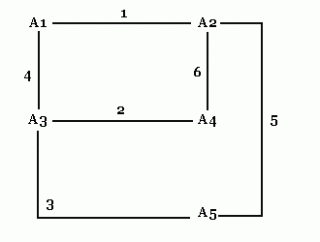
Moguća je i ova shema:

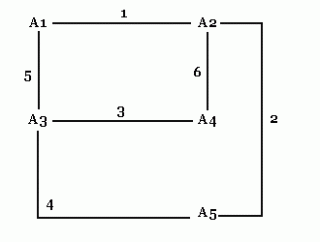
I ovdje je priča ista. Sad već sve vodi prema ovoj shemi:

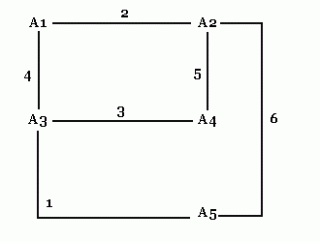
Dakle, peta stanica(A5) obavi razgovor sa jednom od ove četiri, onda po šabloni iz prvog primjera(n=4) u četiri razgovora ove četiri stanice razmijene informacije među sobom, no sada će znati i informacije od stanice A5. Preostaje nam još da petu stanicu(A5) upoznamo sa ovim informacijama, a za to je dovoljno da razgovara sa jednom od ove četiri stanice!
Napokon uviđamo rješenje zadatka:
Imamo n stanica: A1,...,An. Izdvojimo prve četiri stanice (A1,...,A4) i nazovimo ih "glavna grupa". Neka svaka od preostalih n - 4 stanica nazove jednu od prvih četiri i na taj način "injektiraju" svoje informacije u glavnu grupu. Sada stanice u glavnoj grupi razmjene informacije(četiri razgovora) i nakon toga ponovo svaka od preostalih n - 4 stanica nazove jednu od prvih četiri. To je to, bilo nam je potrebno (n - 4) + 4 + (n - 4) = 2n - 4 razgovora, što smo i trebali dokazati.

U rješavanju ovog zadatka najbitniji je moment uočavanje postupka, a čini se da je za to nužno potrebna matematička vještina koja se razvija samo rješavanjem zadataka.

Oznake: matematika

ZADATAK :
Od 200 brojeva: 1, 2, 3,...,199, 200, proizvoljno je izabran 101 broj. Dokazati da se među njima nalaze dva takva da je jedan od njih djeljiv drugim.(Zadatak je preuzet iz knjižice 'Najteži zadaci' iz serije 'Matematika u džepu', a u izdanju 'Tehničke knjige', Beograd)

Kako postaviti ovaj zadatak?
Formulacija zadatka navodi nas da bismo trebali promatrati nekakve skupine (skupove) brojeva koji ne bi trebali ići zajedno, dakle koji bi bili "zavisni" jedni od drugih. Na pamet su mi pale ove: prva skupina: svi brojevi od 1 do 200 djeljivi sa 2, druga skupina: brojevi od 1 do 200 djeljivi sa 3,..., četrnaesta skupina: brojevi od 1 do 200 djeljivi sa 14. Problem je ovih skupova što u svakom od njih postoje dva broja koja mogu ići zajedno( koji nisu "zavisni"): npr: iz skupa 2 brojevi 6 i 14, iz skupa 5 brojevi 15 i 70 itd.

Prije gornjega probao sam sa konkretnom skupinom - uzeo sam brojeve 101-200 kojih ima stotinu i sigurno nisu djeljivi jedni sa drugima. Zatim sam od preostalih stotinu(1-100) pokušao ubaciti jednog "nezavisnog" među njih, ali takav se ne može naći. Dakle, ovaj pristup također nije dobar.
Opet se vraćam na prvi algoritam rješavanja - pronaći skupove međusobno "zavisnih"(djeljivih) brojeva, ovog puta radim novu strukturu skupova:

1. grupa: 1, 2, 4, 8, 16, 32, 64, 128
2. grupa: 3, 6, 12, 24, 48, 96, 192
3. grupa: 5, 10, 20, 40, 80, 160
4. grupa: 7, 14, 28, 56, 112
5. grupa: 9, 18, 36, 72, 144
6. grupa: 11, 22, 44, 88, 176
7. grupa: 13, 26, 52, 104
8. grupa: 15, 30, 60, 120
9. grupa: 17, 34, 68, 136
10. grupa: 19, 38, 76, 152
11. grupa: 21, 42, 84, 168
12. grupa: 23, 46, 92, 184
13. grupa: 25, 50, 100, 200
14. grupa: 27, 54, 108
15. grupa: 29, 58, 116
.
.
.
25. grupa: 50, 100, 200

26. grupa: 51, 102
27. grupa: 53, 106
28.grupa: 55, 110
.
.
50. grupa: 99, 198
51. grupa: 101
52. grupa: 103
.
.
.
99. grupa: 197
100. grupa: 199

Vidimo da ovakvih grupa ima točno sto. Jasno je da ako izaberemo proizvoljnih 101 broj, dva moraju pasti u istu grupu, a time će biti i djeljivi.

Ovime smo riješili zadatak, no postoji li jednostavnije rješenje?

Posežem za rješenjem autora - on polazi od zanimljivog teorema: svaki paran broj može se prikazati kao m × 2**k , gdje je k prirodan broj, a m neparan prirodni broj.
Da li smo mogli ovo sami postaviti svojom intuicijom, ili smo to morali već negdje pročitati? Može li se intuicija steći ili se čovjek s njom rodi? Vjerujem da svatko od nas može naći odgovor na to pitanje.

Dakle, da nastavimo:
Neka je S101 skup od 101 proizvoljnog broja od 1 do 200. Rekli smo da se svaki parni broj može napisati kao m x 2 **k. Označimo sad sa E101 skup koji čine brojevi mj i svi neparni brojevi iz skupa S101. Taj skup ima točno 101 element i svi elementi tog skupa su neparni brojevi manji od 200. Kako među prvih 200 brojeva imamo točno sto neparnih, slijedi da u skupu E101 imamo bar dva jednaka broja. Sad opet imamo tri mogućnosti:
1. U skupu S101 imamo dva parna broja oblika m x 2**r i m x 2**s , njihov količnik biti će 2**(r-s) ili 2**(s-r), u oba slučaja prirodan broj.
2. U skupu S101 imamo neparan broj m i paran broj oblika m x 2**r , količnik je u ovom slučaju m.
3. U skupu S101 imamo dva ista neparna broja, oni su djeljivi jedan sa drugim.

Oznake: matematika, zadaci

Zadatak:
Na šahovskom turniru sudjelovali su samo majstori i velemajstori. Svaki šahist je točno polovicu svojih bodova osvojio u partijama s majstorima. Dokazati da je broj šahista na tom turniru potpun kvadrat.(Zadatak je preuzet iz knjižice 'Najteži zadaci' iz serije 'Matematika u džepu', a u izdanju 'Tehničke knjige', Beograd)

Da se prisjetimo bodovanja šahovskih partija: partija može završiti pobjedom jednog igrača, pri čemu pobjednik dobija jedan bod, a poraženi nula bodova, a može i završiti remijem, pri čemu oba igrača dijele pola boda. Ukupno je dakle u jednoj partiji osvojen jedan bod.
Mi ne možemo znati koliko će koji pojedinac osvojiti bodova, znamo samo da će pola ukupnih bodova osvojiti u partijama s majstorima.
Probajmo zato promatrati bodove po 'grupama', tu bismo već mogli nešto zaključiti. Pri tom mislim na to da majstore promatram posebno i velemajstore posebno.
Uzmimo da je na turniru bilo m majstora i n-m velemajstora, gdje je n ukupan broj šahista. Po uvjetu zadatka, majstori su( kao i velemajstori) polovicu svojih bodova osvojili u partijama sa majstorima, dakle međusobno. Ovdje su osvojili mx(m-1)/2 bodova, a isto toliko osvojili su i u borbi sa velemajstorima. Slično zaključujemo da su velemajstori jednaki broj bodova osvojili u borbi s majstorima kao i međusobno, dakle (n-m)x(n-m-1)/2 bodova. U međusobnim partijama majstori i velemajstori osvojili su nx(n-m) bodova jer je toliko bilo partija pa dobivamo jednakost:

m x(m-1)/2 + (n-m) x(n-m-1)/2 = n x (n-m). Oduvuda dobijamo: (2m- n) = n**2, što je i trebalo dokazati.

Mogli smo i ovako rezonirati:
Uzmimo da imamo m majstora i v velemajstora. Promatramo li bilo kojeg majstora, on je polovinu svojih poena osvojio u partijama sa velemajstorima, dakle u susretima majstori-velemajstori. Uzmemo li nekog velemajstora, on je polovicu poena osvojio također u tim partijama. Izlazi da je pola ukupnih poena osvojeno u tim partijama kojih je bilo m x v. Ukupan broj osvojenih bodova na turniru jest nx(n-1)/2 = (m+v)x(m+v-1)/2 pa imamo jednakost: 2 m x v = (m+v)x(m+v-1)/2, iz čega dobijemo n = (m – v)**2, što je i trebalo dokazati.

Oznake: matematika, zadaci

ZADATAK:
Dvije seljanke donijele su na tržnicu ukupno 100 jaja, jedna više nego druga i obje su za prodana jaja dobile iste svote. Prva reče drugoj: 'Kada bih imala toliko jaja koliko ti, dobila bih za njih 15 krajcara'. Druga joj odgovori: ' A kada bih ja imala toliko jaja koliko ti, dobila bih za njih 6 2/3 krajcara'. Koliko je jaja imala svaka od njih?
(Zadatak je preuzet iz časopisa za mlade matematičare 'Matka' –br.7, ožujak 1994, inače se radi o zadatku koji je Stendhal naveo u svojoj autobiografiji o godinama svojeg školovanja, a o čemu je napisao slijedeće: 'U njega sam našao(Eulerov udžbenik Uvod u algebru) zadatak o broju jaja koje je seljanka nosila na tržnicu da ih proda... Taj je zadatak za mene pravo otkriće. Shvatio sam što znači koristiti oruđe koje se zove algebra. Vrag da me nosi, ali o tome mi nitko dosad nije govorio...')

Ovaj zadatak mogli bismo početi rješavati na ovaj način:
Uzmimo da prva seljanka ima n jaja, a druga 100-n jaja. Neka je prva seljanka prodavala jaja po cijeni c1, a druga po cijeni c2 krajcara. Obje su dobile iste svote novca pa vrijedi:
n× c1=(100-n) × c2. Kada bi seljanke zamijenile broj jaja, a zadržale istu cijenu, vrijedilo bi:
n× c2=15 i (100-n) × c1=62/3=20/3. Ovime smo dobili sustav od tri jednadžbe sa tri nepoznanice, koji, prikazujući c1 i c2 preko n, svodimo na kvadratnu jednadžbu n**2-360n+18000=0 koja nema cjelobrojno rješenje.
Očito smo odveli zadatak u neželjenom smjeru.
Za uspješno rješavanje ovog zadatka potrebno je krenuti na sličan način kao i maloprije. Znamo da su seljanke dobile iste svote novca pa vrijedi n× c1=(100-n) × c2. Ovdje nam sad upada u oči omjer, jer transformacijom jednadžbe dobivamo izraz c1/c2=(100-n)/n=k, koji možemo interpretirati kao omjer cijena, ali i kao omjer broja jaja. Nadalje rezoniramo: ako je prva seljanka imala k puta više jaja od druge, očito je morala prodavati jaja po k puta nižoj cijeni od druge da bi obje jednako zaradile. ( Pritom je zanimljivo da nam izraz 100-n zasad ne igra puno, omjer jaja možemo dobiti i bez njega! )
Sada zaključujemo dalje: ako prva seljanka koja ima k puta više jaja prodaje jaja po cijeni druge seljanke koja je k puta veća od njezine, izlazi da će ona zaraditi k×k=k˛ puta više od druge seljanke. Dakle imamo: k**2=15: 62/3=9/4, iz čega slijedi k=3/2. Vidimo da je prva seljanka imala 3/2 puta više jaja od druge, što bi na jeziku omjera značilo da su jaja među njima bila podijeljena u omjeru 3:2. I tek sada ona brojka od 100 jaja dobiva ulogu, zaključujemo da prva seljanka ima 60, a druga 40 jaja.
I to je to, vidimo da je glavno polazište za rješavanje ovog zadatka bilo uočavanje omjera.

Oznake: matematika, zadaci

ZADATAK 1
U jedno turističko mjesto doputovalo je 100 turista. Od svih njih, 10 nije znalo ni njemački ni francuski jezik, 75 ih je znalo njemački, 85 je znalo francuski. Koliko turista je znalo oba jezika: francuski i njemački? (Zadatak je preuzet iz knjige: '500 odabranih i rešenih zadataka iz matematike', Angelov, Branković, Beograd, 1990)


Jedan lakši zadatak, ali po mom mišljenju dobar pokazatelj vaše 'matematičke' jasnoće misli. Ukoliko lako riješite ovaj zadatak, vrlo vjerojatno ste nadareni za matematiku.

Da krenemo sa rješavanjem:
Deset osoba ne govori ni njemački ni francuski, znači da preostalih 90 govori bar jedan od ova dva jezika.
Od tih 90, njih 75 govori njemački, dakle preostalih 15 ne govori njemački pa zaključujemo da oni govore francuski(i samo francuski). Analogno dobijemo da samo njemački jezik govori 90 – 85 = 5 ljudi.
Znamo da 75 ljudi govori njemački, sada smo doznali da 5 ljudi govori samo njemački, proizlazi da 75 – 5 = 70 ljudi govori i njemački i francuski ( ovu brojku mogli smo dobiti i preko ljudi koji govore francuski: 85 – 15 = 70).
Dakle, 70 ljudi govori i njemački i francuski, 5 ljudi govori samo njemački, 15 samo francuski i 10 ljudi ne govori ni njemački ni francuski.

Oznake: matematika, zadaci