Matematika za svakoga

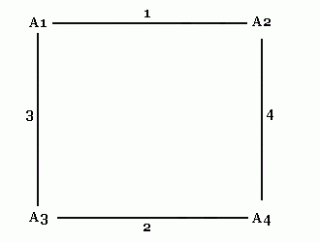
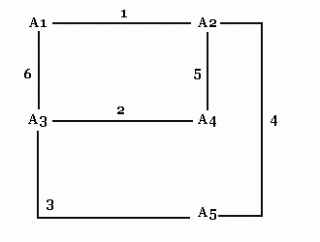
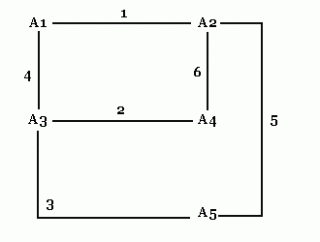
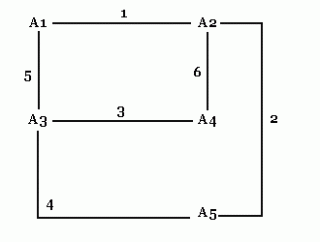
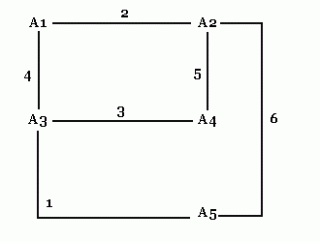
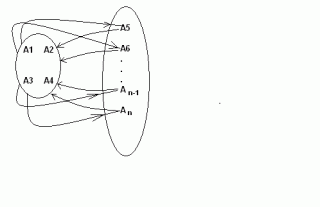
U nekom gradu postoji n policijskih postaja( n>=4). U svakoj znaju po neki podatak važan za hvatanje nekog kriminalca. Dokazati da poslije 2n - 4 telefonskih razgovora sve postaje mogu znati sve podatke. (U jednom razgovoru sudjeluju samo dvije postaje.)(Zadatak je preuzet iz knjižice 'Najteži zadaci' iz serije 'Matematika u džepu', a u izdanju 'Tehničke knjige', Beograd)

Postavljanje zadatka:
- Jasno je da kad dvije stanice "razgovaraju", jedna na drugu prenesu svoje informacije.
- Također je jasno da postaja A može doći do informacija postaje B bez međusobnog kontaktiranja, a preko treće stanice C koja je već kontaktirala s jednom od njih.

Na osnovi ovih postavki postavljam prvi model rješavanja:
Imamo stanice A1, A2,..., An. Uzmimo da prva stanica A1 razgovara sa preostalih n-1 stanica. Nakon razgovora sa posljednjom stanicom An, prva i posljednja stanica raspolažu sa svim potrebnim informacijama. Sada je dovoljno još da prva stanica opet razgovara sa svim stanicama osim posljednje (An) koja već sve zna, da bi sve stanice doznale sve informacije.
Po ovom modelu potrebno je (n-1) + (n-2) = 2n - 3 razgovora, no to nije rješenje zadatka! Mi tražimo broj 2n-4!

Nemam nikakve ideje, zato krećem od najjednostavnijeg primjera kada imamo četiri stanice(n=4). Lako je vidjeti da je dovoljno obaviti 4 razgovora za potpunu razmjenu informacija, a to odgovara formuli: 2 x 4 - 4 = 4. Pogledajmo sliku:

Zatim nastavljam sa n=5. Shema je ova:

Brojevi na linijama označavaju redoslijed razgovora. Vidljivo je da četiri stanice nisu odmah obavile onih četiri razgovora - nakon prva dva razgovora, A2 i A3 su kontaktirali sa A5 i tek nakon toga razgovarali su A1 sa A3 i A2 sa A4. Razmišljajući dalje, uočavam da sam mogao i promijeniti redoslijed razgovora sa istim učinkom, dobivam slijedeću shemu:

I ovdje prije "kompletiranja" prve četiri stanice radim razgovore sa A5.

Moguća je i ova shema:

I ovdje je priča ista. Sad već sve vodi prema ovoj shemi:

Dakle, peta stanica(A5) obavi razgovor sa jednom od ove četiri, onda po šabloni iz prvog primjera(n=4) u četiri razgovora ove četiri stanice razmijene informacije među sobom, no sada će znati i informacije od stanice A5. Preostaje nam još da petu stanicu(A5) upoznamo sa ovim informacijama, a za to je dovoljno da razgovara sa jednom od ove četiri stanice!
Napokon uviđamo rješenje zadatka:
Imamo n stanica: A1,...,An. Izdvojimo prve četiri stanice (A1,...,A4) i nazovimo ih "glavna grupa". Neka svaka od preostalih n - 4 stanica nazove jednu od prvih četiri i na taj način "injektiraju" svoje informacije u glavnu grupu. Sada stanice u glavnoj grupi razmjene informacije(četiri razgovora) i nakon toga ponovo svaka od preostalih n - 4 stanica nazove jednu od prvih četiri. To je to, bilo nam je potrebno (n - 4) + 4 + (n - 4) = 2n - 4 razgovora, što smo i trebali dokazati.

U rješavanju ovog zadatka najbitniji je moment uočavanje postupka, a čini se da je za to nužno potrebna matematička vještina koja se razvija samo rješavanjem zadataka.

Oznake: matematika