Vrednovanje opcija
Jedan od težih izazova u financijama jest kako odrediti vrijednost opcije. Ovdje ćemo opisati najjednostavniji slučaj, a to je određivanje vrijednosti call opcije na dionicu.
Kad želimo kupiti ili prodati opciju, najprije moramo odrediti njezinu vrijednost. To najčešće radimo temeljem objektivnih prametara kojima raspolažemo i subjektivne procjene. Ako je procijenjena vrijednsot opcije manja od njezine tržišne cijene, opcija je za nas precijenjena i treba je prodati. Obrnuto, ako je procijenjena vrijednost opcije veća od cijene na tržištu, opcija je podcijenjena i treba je kupiti. No, krenimo s osnovama.
Sadržaj ovog posta je slijedeći:
- definirat ćemo call opciju na dionicu
- na intuitivan način objasniti ćemo vrijednost opcije i očemu ona ovisi
- objasnit ćemo svrhu modeliranja vrijednosti opcija;
- objasnit ćemo principe vrednovanja opcije koji se koriste u binomnom i Black Scholes Merton modelu
U slijedećem postu obradit ćemo binomni i BSM model vrednovanja, zajedno sa primjerima.
Cilj posta je objasniti slijedeće:
- call opciju
- intrinsična i vremenska vrijednost opcije
- model vrijednosti opcije te varijable i parametre modela
- vjerojatnost neosjetljivu na rizik (risk neutral probability)
Definicija call opcije
Kupnjom call opcije, kupac (odnosno imatelj) stjeće pravo (ali ne i obvezu) kupnje neke vrijednosnice po unaprijed određenoj (ugovorenoj) cijeni, po isteku dogovorenog roka (dospijeća). To znači da može kupiti vrijednosnicu po toj cijeni ako to želi. S druge strane, izdavatelj opcije ima obvezu (a ne pravo) po dospijeću prodati dionicu kupcu na njegov zahtjev po ugovorenoj cijeni. Za stjecanje tog prava, kupac opcije plaća izdavatelju naknadu koja je u biti jednaka cijeni opcije.
Kupac će po dospijeću opcije (odnosno po završetku ugovorenog roka dospijeća) izvršiti opciju, odnosno od izdavatelja opcije tražiti da mu proda dionicu po dogovorenoj cijeni. To će učiniti jedino kad je ugovorena cijena dionice MANJA od tržišne cijene dionice u trenutku dospijeća. Kupac tada stjeće dionicu po cijeni koja je manja od tržišne, a njenom prodajom ostvaruje zaradu u visini razlike trenutne tržišne i ugovorene cijene. Ako je ugovorena cijena dionice VEĆA (koliko veća ili manja definirat ćemo kasnije) od trenutne tržišne cijene dionice, kupac neće izvršiti opciju odnosno tražiti prodavatelja da mu proda tu dionicu po ugovorenoj cijeni. Razlog tome je taj što može kupiti tu istu dionicu na tržištu po nižoj cijeni.
Da rezimiramo, gore opisana call opcija određena slijedećim obaveznim parametrima:
- određena dionica na opciju (ponekad se naziva i odnosna varijabla),
- rok dospijeća (rok nakon kojega kupac može ostvariti svoje pravo, odnosno kupiti dionicu)
- ugovorena cijena (cijena po kojoj kupac može kupiti dionicu)
- tržišna (trenutna) cijena dionice - cijena dionice, o kojoj ovisi vrijednost opcije.
Intuitivno određivanje vrijednosti opcije.
Vrijednost opcije vrlo je jednostavno odrediti po isteku roka dospijeća. Ako je po isteku roka dospijeća razlika između tržišne i ugovorene cijene dionice pozitivna, vrijednost opcije jednaka je upravo toj razlici. Ako je ta razlika negativna, vrijednost opcije je nula (jer kupac neće izvršiti tj. realizirati opciju). Vrijednost opcije po dospijeću naziva se i intrinsična vrijednost.
Ako možemo sa sigurnoću odrediti vrijednost opcije po njezinu dospijeću, postavlja se pitanje kolika je vrijednost opcije tijekom perioda od trenutka izdavanja (odnosno kupnje) do dospijeća? Veća ili manja? Naglašavam da vrijednost opcije prije dospijeća ne možemo odrediti sa sigurnošću. No, sa sigurnošću možemo reći da je vrijednost te opcije prije dospijeća veća od intrinsične vrijednosti. Zašto je tome tako?
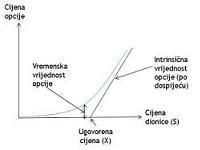
Uzmimo na primjer da je cijena dionice dan prije dospijeća opcije jednaka ugovorenoj cijeni. Intrinsična vrijednost jednaka je nuli. Pravu vrijednost možemo dobiti kao očekivanu (srednju vrijednost) između dva slučaja. Da cijena dionice naraste (npr. za 1) i padne (npr. za -1). U prvom slučaju vrijednost opcije bila bi jednaka 1, a u drugom slučaju vrijednost opcije bila bi jednaka 0. Ako bi obje vrijednosti dionice bile jednako vjerojatne, vrijednost opcije bila bi jednaka 0,5. Ovu bi vrijednost još trebalo diskontirati za 1 dan, prema bezrizičnoj kamatnoj stopi. Dakle, iz ovog vidimo da je vrijednost opcije prije dospijeća veća od intrinsične vrijednosti. Ova razlika između intrinsične i stvarne vrijednosti opcije naziva se vremenska vrijednost - vidi sliku gore.
Spomenuli smo da prije dospijeća vremensku vrijednost opcije ne možemo sa sigurnošću odrediti. To znači da ne možemo odrediti niti ukupnu vrijednost opcije. O čemu zapravo ovisi vrijednost opcije prije njezina dospijeća? Vrijednost opcije ovisi o volatilnosti i trenutnoj tržišnoj vrijednosti dionice, roka dospijeća, ugovorene cijene i kamatne stope. Što je volatilnost dionice (odnosno vjerojatnost odstupanja buduće cijene od trenutne cijene) veća, to je veća mogućnost da tržišna cijena nadmaši ugovorenu cijenu pa stoga i očekivana vrijednost opcije mora biti veća. Što je tržišna cijena veća od ugovorene cijene, očekivana vrijednost opcije je također veća. Što je vrijeme do dospijeća kraće, to je mogućnost da tržišna cijena bude iznad ugovorene cijene manja. Što je ugovorena cijena veća (npr. veća od tržišne), to je vrijednost opcije manja. Što je kamatna stopa veća, to je sadašnja vrijednost opcije manja jer se očekivana vrijednost diskontira po većoj kamatnoj stopi.
Na gornjoj slici možemo vidjeti da se vrijednost opcije sve više približava njenoj intrinsičnoj vrijednosti što je tržišna cijena dionice udaljenija od ugovorene cijene (više ili manje). To znači da je vremenska vrijednost opcije u ta dva slučaja manja. Vremenska vrijednost pokazuje dakle vjerojatnost s kojom će vrijednost opcije biti veća od njezine intrinsične vrijednosti.
Modeli vrednovanja opcije
U prethodnom dijelu intuitivno smo objasnili vrijednost opcije i faktore o kojima ta vrijednost ovisi. Međutim, u praksi, financijske institucije koje trguju opcijama moraju na neki način kvantificirati tu vrijednost. Vrijednost opcije možemo odrediti jedino pomoću modela.
U načelu, model vrednovanja opcije određuje vrijednost opcije u odnosu na cijenu dionice i vrijeme do dospijeća (to su u modelu varijable), a prema roku dospijeća, ugovorenoj vrijednosti, vrsti opcije i volatilnosti dionice (to su u modelu parametri).
Rok dospijeća, ugovorena vrijednost i vrsta opcije su fiksni i moguće ih je nedvojbeno (sa sigurnošću odrediti). Jedino volatilnost cijene dionica ne možemo odrediti sa sigurnošću. Volatilnost predstavlja mjeru vjerojatnosti realizacije cijena dionice o dospijeću opcije. Ovu tzv. buduću volatilnost ne možemo odrediti sa sigurnošću, već je možemo procijeniti temeljem povijesnih parametara, projekcija ili očekivanja.
Model je dakle aproksimacija stvarnosti. Cijena opcije koju predviđa model uglavnom će se razlikovati od stvarne cijene. Razlog tome mogu biti pogreške u modelu (tj. postavke modela nisu realne) ili pogreške u parametrima (parametri nisu točno procijenjeni). No, iz tog razloga, kvalitetan model mora pokazati koliko će se promijeniti vrijednost opcije (output modela), ako smo pogrešno procijenili neki od parametra (npr. što koliko će se promijeniti vrijednost opcije, ako je volatilnost umjesto 20% bude 30%)?
Principi vrednovanja opcije
U ovom dijelu objasnit ćemo 3 osnovna principa vrednovanja opcije. Prvi princip koristi očekivane vrijednosti i premiju za rizik. Drugi princip koristi tzv. vjerojatnost neosjetljivu na rizik i koristi se u binomnom modelu. Treći princip radi na principu konstruiranja portfolia koji je neosjetljiv na rizik i koristi se u Black Scholes Merton-ovom (BSM) modelu. Binomni i BSM modeli biti će objašnjeni u slijedećem poglavlju.
Sva 3 principa ilustrirat ćemo na slijedećem pojednostavljenom primjeru. Cijena dionice je €100. Zadatak je odrediti vrijednost opcije u trenutku t=0 na tu dionicu za rok dospijeća t=T uz ugovorenu cijenu €100. Pretpostavljamo dodatno da su u trenutku t=T moguće samo dvije cijene: €101 (sa vjerojatnošću 60%) i €99 (sa vjerojatnošću 40%). Pretpostavimo i da je diskontna stopa jednaka nuli.
Primjer koji ilustrira navedene principe možete preuzeti ovdje.
Vrednovanje opcije pomoću premije za rizik
Pretpostavljamo da će vrijednost opcije u trenutku t=0 biti jednaka diskontiranoj očekivanoj (tj. srednjoj) vrijednosti u dva slučaja: prvi kad je cijena dionice €101 i drugi kad je cijena dionice €99. U prvom slučaju, zarada od opcije je €1, a u drugom slučaju €0. Ako bi opciju vrednovali prema očekivanoj (srednoj) vrijednosti njezina bi vrijednost bila: €1x0,6 €0x0,4=€0,6, tj vrijednost opcije bila bi €0,6.
Međutim, u tom slučaju, ne bi uzeli u obzir premiju za rizik odnosno premiju za mogućnost da ne dobijemo ništa ili da zaradimo €1. Očekivani prinos na dionicu bio bi u tom slučaju jednak nuli pa ne bi bilo kompenzacije za rizik. Ako bi uzeli u obzir premiju za rizik, vrijednost opcije bi trebala biti nešto manja od €0,6.
U slučaju dionice, premija za rizik je razlika između očekivane vrijednosti koja iznosi €101x0,6 €99x0,4=€100,2 i cijene dionice koja iznosi €100. Znači, premija za rizik kod dionice iznosi €0,2. Premija za rizik kod opcije trebala bi biti proporcionalna riziku dionice. Rizik kod dionice jednak je razlici moguće cijene u spomenuta dva slučaja (tj. €101-€99=€2), dok je rizik kod opcije jednak €1-€0=€1. Budući da je raspon vrijednosti (tj. rizik) opcije dvostruko manji od raspona vrijednosti dionice, premija za rizik kod opcije također treba biti dvostruko manja, odnosno iznositi €0,2/2=€0,1. Prema tome, vrijednost opcije trebala bi biti €0,6-€0,1=€0,5.
Vrednovanje opcije pomoću vjerojatnosti neosjetljive na rizik
Vrijednost opcije možemo dobiti i na slijedeći način. Ako znamo moguće vrijednosti dionice (i opcije) na kraju razdoblja te na početku razdoblja, možemo izračunati vjerojatnost „p“ kojom kad ponderiramo buduće vrijednosti dionice dobivamo njezinu sadašnju vrijednost. Tako dobivena vjerojatnost naziva se „vjerojatnost neosjetljiva na rizik“. Vjerojatnost neosjetljiva na rizik nema veze sa statističkom vjerojatnošću – to je umjetno stvorena veličina kojom ponderiramo buduće vrijednosti dionice kako bi dobili njenu sadašnju vrijednost. Vrijednost opcije računamo tako izračunamo očekivanu vrijednost opcije ali koristeći dobivenu vjerojatnost neosjetljivu na rizik.
Npr. Ukoliko je trenutna vrijednost dionice 100, a cijene dionica u budućnosti može imati vrijednosti 101 i 99 (sa statističkom vjerojatnošću 60% i 40%), vjerojatnost neosjetljiva na rizik jednaka je 50%, bez obzira na stvarnu vjerojatnost. Dakle: 100 = p x 101 (1-p) x 99 iz čega slijedi p = 50%. Ako je sadašnja cijena dionice jednaka 99,9 (umanjena za diskont). Vrijednost opcije dobivamo ponderiranjem mogućih vrijednosti opcije sa vjerojatnošću neosjetljivom na rizik: V = p x (101-100) (1-p) x 0 = 0,5.
Vrednovanje opcije pomoću vjerojatnosti neosjetljive na rizik koristi se u binomnom modelu koji će biti objašnjen naknadno.
Vrednovanje opcije konstruiranjem portfolia neosjetljivg na rizik
Budući da je promjena cijene kod ove opcije dvostruko manja od promjene cijene dionice, mogli bismo konstruirati portfolio sa dugom pozicijom dionici i kratkom pozicijom dvije opcije na du dionicu. Kratka pozicija u opciji znači da smo prodali pravo (call). Vrijednost tog portfolia bi u slučaju da je cijena dionice €101 bila jednaka: -2x€1 €101=€99. U slučaju da je cijena dionice bila €99, vrijednost portfolia bi iznosila €99 jer bi vrijednost opcije bila jednaka €0. Dakle vrijednost portfolia u trenutku dospijeća opcije je ista bez obzira na cijenu dionice, i iznosi €99. Porast cijene dionice kompenziran je isplatom opcije, dok je u slučaju pada cijene dionice vrijednost opcije jednaka nuli.
Ako je vrijednost portfolia o dospijeću ista u oba slučaja, vrijednost portfolia u trenutku formiranja trebala bi biti također biti ista odnosno umanjena za diskontni faktor DF (a za sada ćemo pretpostaviti da je DF jednak nuli). Ako znamo vrijednost portfolia prilikom njegova formiranja, možemo jednostavno izračunati vrijednost opcije u trenutku njegova formiranja. Vrijednost portfolia dakle iznosi: -2xV €100=€99, gdje V označava vrijednost opcije. Iz ove jednadžbe ispada da je vrijednost opcije V jednaka €0,4. Dakle, izračunata vrijednost opcije jednaka je vrijednosti koju smo izračunali koristeći raspone vrijednosti.
Konstruiravši portfolio dionice i opcije koji je neosjetljiv na rizik promjene cijene dionice, bili smo u mogućnosti izračunati vrijednost opcije (od €0,4) a da uopće ne koristimo vjerojatnosti realizacije pojedine cijene dionica (60% i 40%).
Dakle, ako hoćemo vrednovati opciju pomoću ove metode, radimo slijedeće:
- konstruiramo portfolio dionice i opcija koji je neosjetljiv na rizik
- izračunamo vrijednost portfolia o dospijeću i tu vrijednost diskontiramo
- iz diskontirane vrijednosti portfelja i cijene dionice izračunamo vrijednost opcije
Vrednovanje pomoću portfelja neosjetljivog na rizik koristi se u Black Scholes Merton modelu koji će biti objašnjen kasnije.
Vrijednost opcije ne ovisi o tome hoće li dionica rasti ili padati
Iz prethodnog razmatranja možemo izvući jedan pomalo neintuitivan zaključak, a to je da vrijednost opcije uopće ne ovisi o statističkoj vjerojatnosti porasta ili pada cijene dionice, već o tzv. vjerojatnosti neosjetljivoj na rizik.
Uzmimo slijedeći primjer: kad bi vjerojatnost porasta cijene dionice bila 90%, a pada 10%, očekivana isplata po dospijeću isplata bila bi €1x0,9=0,9. Recimo da je investitor A spreman kupiti opcije po toj cijeni. No, investitor B koji vrednuje opcije prema gornjem modelu uočio bi da je ta opcija precijenjena. Tako bi mogao prodati dvije opcije za €0,9 i kupiti jednu dionicu. Njegov portfolio bi na početku vrijedio €99,8-2x€0,9=€98. Po dospijeću portfolio bi u oba slučaja vrijedio €99, što bi značilo da do dospijeća ostvaruje siguran profit od €1.
Ako bi pretpostavili idealno tržište bez ovakovih (arbitražnih) profita, cijena opcije bi se u ovom slučaju morala spustiti do one granice na kojoj je profit jednak nuli (jer za portfolio bez rizika profit treba biti jednak nuli) - tj. do vrijednosti €0,4 jer bi jedino u tom slučaju profit bio jednak nuli.
To be continued ...
|


