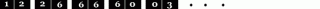Marketing
Domino pločice
Zašto se 28 pločica domina može sastaviti, držeći se pravila igre, u jedan neprekidan lanac?(Zadatak je preuzet iz knjižice 'Zanimljiva matematika', J.I.Pereljman)
Za početak želim se upoznati sa pločicama, složiti nekolicinu, prebrojati ih, matematički naći koliko ih ima. Svaku pločicu možemo promatrati kao (x,y), gdje x i y označavaju broj točkica na jednoj i drugoj strani. Broj može biti od 0 do 6, a imamo i 'duple' pločice sa jednakim brojem na obje strane (x,x). Dva broja na pločici možemo kombinirati na 7 x 6 / 2= 21 načina. Plus to imamo i 7 'duplih' pločica, dakle ukupno imamo 28 pločica.
To je što se tiče broja pločica, no zašto one moraju činiti lanac? Krećem od ideje da spojeve pločica u shemi prikažem sa jednim brojem i tako pojednostavim shemu, npr. red
prikazat ću kao 1-2-6-6-0-3-..., no nakon malo razmišljanja shvaćam da mi to neće baš puno pomoći.
Nastavljam sa blistavijom idejom: počnem slagati lanac od bilo koje pločice, npr. (3,5), potom stavljam duplu (5,5). Duple pločice trudim se iskoristiti što prije! Nastavljam sa (5,0), to su već tri pločice koje sadrže broj 5, ostaje ih još četiri( paran broj). Nastavljam dalje sa (0,0), još jednom duplom pločicom i nadovezujem se sa (0,1). Slično prijašnjem, ostaje još četiri pločica sa brojem 0. Nastavljam na isti način: (1,1) - (1,2) - (2,2) – (2,3) – (3,3) – (3,4) – (4,4) – (4,6) – ( 6,6) – (6,0) , sve duple su mi sada iskorištene! Sada, uzmemo li ma koji broj od 0 do 6, ostaje nam paran broj pločica sa tim brojem(npr. sa brojem 4 ostale su nam (0,4), (1,4), (2,4) i (5,4)). Izuzetak su broj 3 ( prva pločica) i 0 (zadnja pločica) koji se očito dalje nastavljaju. Intuicija nam govori da će se prva i posljednja pločica na kraju spojiti... Ovo već je nekakav algoritam za rješavanje, no možemo li ga pojednostaviti?
Probajmo tako da 'duple' pločice ostavimo za kraj – tada ih jednostavno ubacimo između dvije pločice sa tim brojem, npr. (3,3) ubacimo između (4,3) i (3,0). Problem smo dakle sveli na slaganje 'normalnih' 21 pločica. Znamo da od svakog broja imamo 6 pločica i jasno je da uzmemo li bilo koje dvije susjedne pločice u lancu, one spadaju u istu grupu (sa tim brojem) i nedostaje ih još paran broj. Također je jasno da, kako nastavljamo lanac, uvijek mora postojati domino pločica za nastavak, upravo zbog tog parnog broja pločica. I stoga ponovo intuitivno zaključujemo da se zadnja polčica mora nadovezati na prvu, tj. lanac mora biti zatvoren!
Jedno pitanje ostaje neriješeno – hoćemo li na ovaj način uspjeti potrošiti sve pločice domina- njih 21(bez duplih)?
Probajmo pokazati da možemo.
Uzmimo da se to ne može, dakle možemo sastaviti maksimalno n pločica, gdje je n<21. Uzmimo prvo da lanac počinje sa (x,y), a završava sa (r,s), x <> s. Zbog parnog broja pločica po grupama jasno je da niz možemo nastaviti i s jedne i s druge strane, što je kontradikcija!
Sada uzmimo da lanac počinje sa (x,y), a završava sa (z,x) i pretpostavimo da u lancu nedostaje pločica (r,s). U lancu mora postojati mjesto (p,r) – (r,q) , jer kad ne bi postojalo, onda bi sve pločice sa brojem r bile izvan lanca, među njima i pločica (r,x) . Tada bi raskinuli lanac na (z,x)-(x,y) i tu nadovezali (r,x), što je kontradikcija. Dakle, na mjestu (p,r) – (r,q) raskinemo lanac i ubacimo pločicu (r,s) čime produžujemo lanac, što je opet kontradikcija. Ovime smo dokazali da možemo iscrpiti svih 21 pločica.
Post je objavljen 12.07.2015. u 21:15 sati.